DP
状压DP
首先回顾一下位运算
- 与 &
-
或 - 异或 ^
- 取反 ~
- 左移 «
- 右移 »
^ 运算的逆运算是它本身
取反是对 1 个数 $num$ 进行的计算,~ 把$num$种的0 和 1 全部取反 补码——正数的补码是其(二进制) 本身,负数的补码是其(二进制)取反后加一
右移在C++中将直接舍弃右侧多余位,左侧则较为复杂,无符号数会在左侧补0,对于有符号书,则会用最高位的数补齐
[注]:
1. 左移和右移是有返回值的,并非对$num$本身进行操作
2. 左移和右移优先级低于四则运算,x<<1+1 会被解释为x<<(1+1),所以一般最好都加上括号
一些应用
num<<i相当于$num\times 2^i$ ,而num>>i相当于$num \div 2^i$ 。效率要比 % 和 / 操作快得多(60%?)- 当$num>0$时两者并没有差别,但是当$num<0$时,普通除法时向0取整,而右移是向下取整
num * 10 = (num << 1) + (num << 3)- num & 1 取num二进制末尾,判断奇偶性
- 对应于集合上的运算
| 操作 | 集合表示 | 位运算语句 |
|---|---|---|
| 交集 | $a\cap b$ | a&b |
| 并集 | $a\cup b$ | a |
| 补集 | $\overline a$ | ~a |
| 差集 | $a\setminus b$ | ~a |
| 对称差 | $a\triangle b$ | a^b |
//遍历一个集合的子集
for(int S0 = S;S0;S0 = (S0-1) & S)
//取出n二进制下的第k位
(n >> k) & 1
//取出整数n在二进制表示下第0~k-1位(后k位
n & ((1<<k) - 1)
//把整数n在二进制下的第k位取反
n ^ (1 << k)
//对整数 n 在二进制下第k位赋值1
n | (1 << k)
//对整数 n 在二进制表示下第k位赋值0
n & (~(1 << k))
//判断一个数的奇偶性
bool isOddNumber(int n){
return n & 1;
}
//判断一个数是不是2的幂
bool isFactorialofTwo(int n){
return n > 0 && (n & (n-1)) == 0;
}
好了开始正题
状压DP是DP的一种,通过状态压缩为整数来优化转移 直接上题 题目链接 在$N\times N$ 的棋盘里面放 $K$个国王,使他们互不攻击,共有多少种摆放方案。国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一个格子,共$8$ 个格子。 $1\le N\le 9,0\le K\le N*N$ $f(i,j,l)$来表示前 $i$ 行,当前状态为$j$ ,且已经放置 $l$个国王时的方案。 $j$ 这一维用二进制来表示 先预处理在一行上的所有合法状态(即排除同一行上两个相邻的情况),然后直接枚举这些来匹配上一行的状态即可。 $f(i,j,l) = \sum f(i-1,x,l-num(x))$ $num(x)$ 为x在二进制下有多少个1 转移时要排除两行间国王互相攻击不合法的情况。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
vector<int> sta,stan;
ll d[10][(1<<10)][100];
int n,k;
bool ok(int i,int j){
if(i & j)return false;
if((i << 1) & j)return false;
if(i & (j << 1))return false;
return true;
}
int main(){
scanf("%d%d",&n,&k);
for(int i=0;i<(1<<n);i++){
int num = 0;
bool flag = true;
for(int j=0;j<n-1;j++){
if(i >> j & 1){
num++;
if(i >> (j+1) & 1){
flag = false;
break;
}
}
}
if(!flag)continue;
sta.push_back(i);
stan.push_back(num + (i >> (n-1) & 1));
}
for(int i=0;i<sta.size();i++){
d[1][i][stan[i]] = 1;
}
for(int i=2;i<=n;i++){
for(int j=0;j<sta.size();j++){
for(int t=0;t<sta.size();t++){
if(ok(sta[j],sta[t])){
for(int p = stan[j];p <= k;p++){
d[i][j][p] += d[i-1][t][p-stan[j]];
}
}
}
}
}
ll res = 0;
for(int i=0;i<sta.size();i++)
res += d[n][i][k];
cout<<res<<endl;
return 0;
}
不过瘾就再来一道
Mondriann’s Dream 求把$N*M(1\le N,M \le 11)$ 的棋盘分割成若干个$1\times 2$ 的长方形,有多少种方案。例如当 $N=2,M=4$时,共有5种方案。当$N=2,M=3$时,有3种方案。
NM只有11,八九不离十可以状压了,反正得挨个铺,所以从上到下考虑。假如现在铺好了前$i$ 层,基本思想就是从$i$ 层的状态转移到$i+1$层的状态。但是该如何表示?观察一下铺满第 $i$ 层的样子(必须保证第$i$层是满的,也就是说有的可以凸出来到$i+1$层但是要保证$i$层是满的)
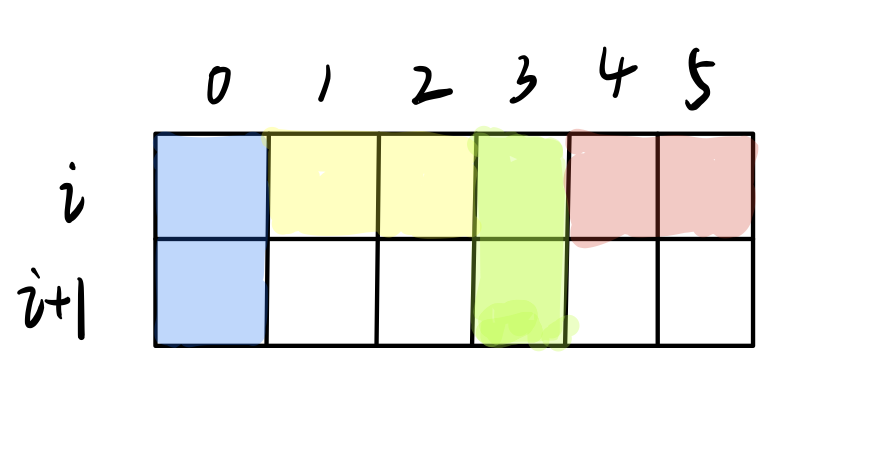 对于第 i 行中竖着放的,第 $i+1$ 层要受到牵连,它必须补全竖着放置的上一半才行。但对于横着放的,第$i+1$层则无所谓。
所以我们可以用二进制中的 1 来表示他是否是竖着放置的上一半。为0则为其他状况。
$d[i][j]$表示第 $i$ 的形态为$j$ 时,前$i$ 行分割方案的总数。 $j$ 是用十进制整数记录的 $m$ 位二进制数。考虑$i+1$行的状态$k$在满足什么情况下转移是合法的。
对于第 i 行中竖着放的,第 $i+1$ 层要受到牵连,它必须补全竖着放置的上一半才行。但对于横着放的,第$i+1$层则无所谓。
所以我们可以用二进制中的 1 来表示他是否是竖着放置的上一半。为0则为其他状况。
$d[i][j]$表示第 $i$ 的形态为$j$ 时,前$i$ 行分割方案的总数。 $j$ 是用十进制整数记录的 $m$ 位二进制数。考虑$i+1$行的状态$k$在满足什么情况下转移是合法的。
- $j$中为 1 的位,$k$中必须为0
- $j$中为 0 的位,$k$中可以为1,但 k 要是为 0,就必须是连续的偶数个0(想一想为什么) 对于第一条,可以用 $i\&j = 0$ 来判断,对于第二条,有$z = i|j$,那么 z 的二进制表示中,每一段连续的 0 都必须有偶数个。(这些0代表若干个横着的 $1\times 2$ 长方形,奇数个0无法分割成这种形态。
#include <iostream>
#include <cstdio>
using namespace std;
int n,m;
long long f[12][1<<11];
bool in_s[1<<11];
int main(){
while(cin>>n>>m && n){
//先把合法状态筛出来,即二进制表示中每一段连续的0都有偶数个
for(int i=0;i<1<<m;i++){
bool cnt = 0,has_odd = 0;
for(int j=0;j<m;j++)
if(i >> j & 1)has_odd |= cnt,cnt=0;
else cnt ^= 1;
in_s[i] = (has_odd | cnt) ? 0 : 1;
}
f[0][0] = 1;
for(int i=1;i<=n;i++){
for(int j=0;j<1<<m;j++){
f[i][j] = 0;
for(int k=0;k< 1<<m;k++){
if((j & k) == 0 && in_s[j|k])
f[i][j] += f[i-1][k];
}
}
}
cout<<f[n][0]<<endl;
}
return 0;
}
数位DP
数位DP问题往往是这样的题型,给定一个闭区间$[l,r]$,让你求这个区间中满足某种条件的数的总数 又或者是求满足限制条件的第K小的数是多少。
- 首先我们将问题转换为更加简单的形式。设$ans_i$ 表示$[1,i]$ 中满足条件的数的数量,那么所求的答案就是$ans_r-ans_{l-1}$。
分开求解这两个问题即可。 对于一个小于$n$的数,它从高到底肯定出现某一位使得这一位上的数值小于$n$这一位上对应的数值。而之前的所有位都和$n$上的位相等。 有了这个性质,我们可以定义$f(i,st,op)$表示当前将要考虑的是从高到低的第$i$位,当前该前缀的状态为$st$(前一位或前几位的值),前缀和当前求解的数字的大小关系是op(op=1表示等于,op=0表示小于)时的数字个数。 题目链接
windy数 windy定义了一种windy数。不含前导零且相邻两个数字之差至少为2的正整数被称为windy数。 windy想知道, 在A和B之间,包括A和B,总共有多少个windy数?$1 \le A \le B \le 2000000000$
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll A,B;
int k[20],pos;//存数字各位
ll dp[20][10];//第i位为j的数字个数(不能大小限制)
/*
pos : 当前考虑的第pos位,例如十进制数12345,5为第0位
pre : 当前位的前一位的数字
lead : 是否有前导0,比如之前枚举的两位 00xxx,在枚举3位时是有前导0的。
limit : 是否有大小限制,比如枚举了12xxx,在枚举3位时最大枚举到3
*/
ll dfs(int pos,int pre,bool lead,bool limit){
if(pos == -1) return 1;
if(!limit && !lead && dp[pos][pre])return dp[pos][pre];
int up = limit ? k[pos] : 9;//确定枚举上界
ll res = 0;
for(int i=0;i<=up;i++){
if(lead){
if(i == 0){
res += dfs(pos-1,0,true,false);
}
else{
res += dfs(pos-1,i,false,limit && i == k[pos]);
}
}else{
if(abs(i-pre) < 2)continue;
res += dfs(pos-1,i,false,limit && i == k[pos]);
}
}
if(!limit && !lead)dp[pos][pre] = res;
return res;
}
ll solve(ll x){
int pos = 0;
while(x){
k[pos++] = x % 10;
x /= 10;
}
return dfs(pos-1,0,true,true);
}
int main(){
scanf("%lld%lld",&A,&B);
printf("%lld\n",solve(B) - solve(A-1));
return 0;
}
Valley Number
当一个数字,从左到右依次看过去数字没有出现先递增接着递减的“山峰”现象,就被称作 Valley Number。它可以递增,也可以递减,还可以先递减再递增。在递增或递减的过程中可以出现相等的情况。
比如,1,10,12,212,32122都是 Valley Number。
121,12331,21212则不是。
度度熊想知道不大于N的Valley Number数有多少。
注意,前导0是不合法的。
每组数据包含一个数N。
● 1≤T≤200
● 1≤length(N)≤100
结果对$1000000007$取模
#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
typedef long long ll;
int T;
ll d[101][11][3];
char s[101];
int k[101],pos;
/*
减后可以增。增后不能减
status :
0 不增不减
1 增
2 减
*/
ll dfs(int pos,int pre,int status,bool lead,bool limit){
if(pos == -1)return lead ? 0 : 1;
if(!lead && !limit && d[pos][pre][status])return d[pos][pre][status];
int up = limit ? k[pos] : 9;
ll res = 0;
for(int i=0;i<=up;i++){
if(lead){
if(i == 0){
(res += dfs(pos-1,0,0,true,false))%mod;
}
else{
(res += dfs(pos-1,i,0,false,limit && i == k[pos]))%mod;
}
}
else{
if(i < pre){
if(status == 1)continue;
(res += dfs(pos-1,i,2,false,limit && i == k[pos]))%mod;
}
else if(i == pre){
(res += dfs(pos-1,i,status,false,limit && i == k[pos]))%mod;
}
else{
(res += dfs(pos-1,i,1,false,limit && i == k[pos]))%mod;
}
}
}
if(!lead && !limit) d[pos][pre][status] = res % mod;
return res;
}
ll solve(){
int n = strlen(s);
pos = 0;
for(int i=n-1;i>=0;i--)k[pos++] = s[i]-'0';
return dfs(pos-1,0,0,true,true);
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%s",s);
printf("%lld\n",solve()%mod);
}
return 0;
}
POJ-3208 启示录 只要某数字的十进制表示中有三个6相邻,则该数字为魔鬼数,求第X小的魔鬼数$X\le 5e7$
这一类题目可以先用DP进行预处理,再基于拼凑思想,用“试填法”求出最终的答案
$F[i,3]$表示由 $i$ 位数字构成的魔鬼数有多少个,$Fi,j$ 表示由 $i$ 位数字构成的,开头已经有连续 $j$ 个6的非魔鬼数有多少个。(允许前导0的存在,想一想为什么) 转移方程
- $F[i,0] = 9*(F[i-1,0] + F[i-1,1] + F[i-1,2])$
- $F[i,1] = F[i-1,0]$
- $F[i,2] = F[i-1,1]$
- $F[i,3] = F[i-1,2] + 10 * F[i-1,3]$
然后一位一位的试填,要注意前面填过的数字结尾如果有 k 个6,通过后面拼接 3-k 个6也可以构成魔鬼数
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
ll f[21][4];
int T,n,l;
void init(){
f[0][0] = 1;
for(int i=1;i<=20;i++){
f[i][0] = 9*(f[i-1][0] + f[i-1][1] + f[i-1][2]);
f[i][1] = f[i-1][0];
f[i][2] = f[i-1][1];
f[i][3] = f[i-1][2] + 10 * f[i-1][3];
}
}
int main(){
init();
scanf("%d",&T);
while(T--){
scanf("%d",&n);
//l为答案的长度
for(l=3;f[l][3] < n;l++);
//k表示填过的数字末尾有k个6
for(int i=l,k=0;i;i--){
for(int j=0;j<=9;j++){
ll cnt = f[i-1][3];//后面预处理出的魔鬼数
//找能够拼凑出来的魔鬼数
if(j == 6 || k == 3){
if(k == 3){
for(int x = 0;x < 3;x++)
cnt += f[i-1][x];
}else{
for(int x = max(3-k-1, 0);x<3;x++){
cnt += f[i-1][x];
}
}
}
if(cnt < n) n -= cnt;
else{
if(k < 3) j == 6 ? k ++ : k=0;
printf("%d",j);break;
}
}
}
cout<<endl;
}
return 0;
}
BZOJ1799 月之迷 给出两个数a,ba,b,求出$[a,b]$中各位数字之和能整除原数的数的个数。 我们按照模板的做法来想,枚举到第pos位时,要确定这一位的数字,可以更新现在所填数字的和,但对于最终的和无从得知,是否能整除也无从判别,我们试着先确定了最终的和,在枚举每一位的时候注意到,枚举x,则对最终和模数可以更新为 $(mod * 10 + x) \% sum$ ,所以可以想到每一次枚举一个和sum $d[i][j][k]$表示 i 位数字,前面填过的数字和为 j 时,模sum为 k 的数字个数
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll d[20][160][160],L,R;
int k[20],pos,mod;
//sum为之前填过的数字的和,p为之后要填的数字对mod的模为p
ll dfs(int pos,int sum,int p,bool lead,bool limit){
if(pos == -1){
if(p == 0 && sum == mod)return 1;
else return 0;
}
if(!limit && !lead && d[pos][sum][p] != -1)return d[pos][sum][p];
int up = limit ? k[pos] : 9;
ll res = 0;
for(int i = 0;i <= up;i ++){
if(lead){
if(i == 0){
res += dfs(pos - 1, sum + i, p, true, false);
}
else {
res += dfs(pos - 1, sum + i, (p * 10 + i) % mod, false, limit && i == k[pos]);
}
}
else {
res += dfs(pos - 1,sum + i, (p * 10 + i) % mod, false, limit && i == k[pos]);
}
}
if(!limit && !lead) d[pos][sum][p] = res;
return res;
}
ll solve(ll x){
pos = 0;
while(x){
k[pos++] = x % 10;
x/=10;
}
ll res = 0;
//mod为当前枚举的和
for(mod=1;mod <= pos * 9;mod++){
memset(d,-1,sizeof d);
res += dfs(pos-1,0,0,true,true);
}
return res;
}
int main(){
scanf("%lld%lld",&L,&R);
//cout<<solve(R)<<' ' <<solve(L-1)<<endl;
printf("%lld\n",solve(R)-solve(L-1));
return 0;
}
计数类DP
直接上题,跟之前的排列组合有比较大的联系
CF-559C Gerald and Giant Chess 给定一个 $H*W$的棋盘,棋盘上只有$N$ 个格子是黑色的,其他格子都是白色的。 在棋盘左上角有一个卒,每一步可以向右或者向下移动一格,并且不能移动到黑色格子中。求这个卒从左上角移动到右下角,一共有多少种可能的路线 $1\le H,W\le 10^5,1\le N\le 2000$ 输出对$10^9+7$取模 H,W巨大,普通DP不用想,考虑如何用黑格子计数
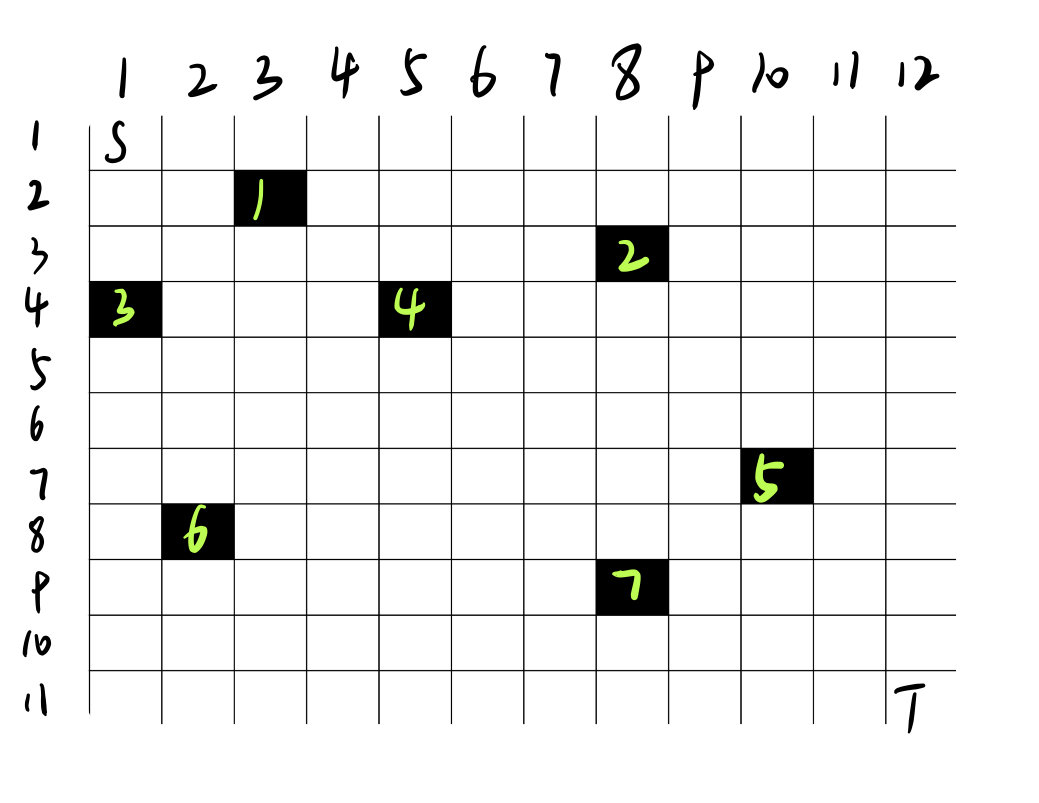
由组合数学知识可知,从S到T的总路径条数为$C_{H+W-2}^{H-1}$,只要减去至少经过一个黑格子的路径条数即为答案。 那么如何不重不漏的计数呢? 考虑每条至少经过一个黑格子的路径所包含的第一个黑格子,以4号黑格子(4,5)为例,从S到4号,总路径条数有$C_{4+5-1-1}^{4-1}$条,只要排除掉经过3和经过1的路径条数即为从S到4,不经过黑格子的路径数。如何排除?其实我们之前已经算出来了,在算S到4的不经过黑格子路径条数时,已经分别算过了S到3,S到1的不经过黑格子路径条数,只要分别乘上由3到4,由1到4的所有路径数即可。
把所有黑色格子按照行列坐标递增的顺序排序,设$f[i]$ 为从S到第 $i$个格子,途中不经过其他黑色格子的路径数 \(f[i] = C_{x_i-1+y_i-1}^{x_i-1} - \sum_{j=1}^{i-1}f[j]*C_{x_i-x_j+y_i-y_j}^{x_i-x_j},其中x_i\ge x_j,y_i\ge x_j\) 在求解计数类动态规划时,通常要找一个“基准点”,围绕这个基准点构造一个不可划分的”整体”,以避免子问题之间的重叠
#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
const int N = 2e5+10;
typedef long long ll;
typedef pair<int,int> pii;
#define fi first
#define se second
ll jc[N],inv[N];
int h,w,n;
ll f[2010];
pii a[2010];
ll ksm(ll a,ll b){
ll res = 1;
for(;b;b>>=1){
if(b & 1)res = res * a % mod;
a = a * a % mod;
}
return res;
}
int C(int x,int y){
return jc[x] * inv[y] %mod * inv[x-y] % mod;
}
int main(){
jc[0] = 1;inv[0] = 1;
for(int i=1;i<N;i++)jc[i] = jc[i-1] * i % mod,inv[i] = ksm(jc[i],mod-2);
scanf("%d%d%d",&h,&w,&n);
for(int i=1;i<=n;i++)scanf("%d%d",&a[i].fi,&a[i].se);
sort(a+1,a+1+n);
a[n+1].fi = h;a[n+1].se = w;
for(int i=1;i<=n+1;i++){
int x = a[i].fi,y = a[i].se;
f[i] = C(x+y-2,x-1);
for(int j=1;j<i;j++){
int xj = a[j].fi;
int yj = a[j].se;
if(xj > x || yj > y)continue;
f[i] = (f[i] - (ll)f[j] * C(x-xj+y-yj,x-xj)%mod + mod)%mod;
}
}
printf("%lld\n",f[n+1]%mod);
return 0;
}
斜率优化DP
P3195 [HNOI2008]玩具装箱TOY
题目链接 设$d[i]$为将前 $i$ 个玩具装入箱中所需得最小费用 容易得到动态转移方程: \(d[i] = min(d[j] + (s[i]-s[j]+i-j-1-L)^2), (j<i)\) 其中$s[i] = \sum_1^iC[i]$,普通DP复杂度为$O(n^2)$。经过斜率优化后将变为$O(n)$。 仔细观察我们便于表示可以令$f[i] = s[i]+i$ 那么式子变成了
\[d[i] = min(d[j] + (f[i]-f[j]-1-L)^2)\]我们讨论$j_1,j_2(1\le j_1< j_2<i)$决策,假设$j_2$要比$j_1$更优,那么有
$d[j_1] + (f[i] -f[j_1]-1-L)^2 \ge d[j_2]+(f[i]-f[j_2]-1-L)^2$
展开后得到
$d[j_1] + f[i]^2 - 2\times f[i]\times (f[j_1]+1+L)+(f[j_1]+1+L)^2 \ge d[j_2]+f[i]^2-2\times f[i]\times (f[j_2]+1+L)+(f[j_2]+1+L)^2$
移项后可得
$2\cdot f[i]\ge {d[j_2]+(f[j_2]+1+L)^2-d[j_1]-(f[j_1]+1+L)^2 \over f[j_2]-f[j_1]}$
令$g[i] = f[i]+1+L$, 则有
$2\cdot f[i]\ge {(d[j_2]+g[j_2])-(d[j_1]+g[j_1])\over f[j_2]-f[j_1]}$
所以用一个队列维护决策集,当$j_1<j_2$,并且上式满足时,$j_1$ 出队。 又由于$f[i]$随$i$单调递增。所以计算$d[i]$之后要将 $i$ 入队时,要及时排除掉不可能作为决策的元素。 如何计算?队尾的斜率也要满足单调性,保持跟$f[i]$的单调性一致即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 50010;
typedef long long ll;
typedef long double db;
db c[N],d[N],f[N],s[N],g[N];
int n,L;
int q[N],l,r;
db sqr(db x){return x * x;}
db slope(int i,int j){
return ((d[i] + g[i]) - (d[j] + g[j])) / (f[i] - f[j]);
}
int main(){
scanf("%d%d",&n,&L);
l=r=1;
for(int i=1;i<=n;i++){
cin>>c[i];
s[i]=s[i-1] + c[i];
f[i] = s[i] + i;
g[i] = (f[i] + 1 + L) * (f[i] + 1 + L);
}
g[0] = (ll)(1+L)*(1+L);//注意0号元素的g值初始化
for(int i=1;i<=n;i++){
while(l < r && slope(q[l],q[l+1]) < 2 * f[i])l++;
int j = q[l];
d[i] = d[j] + sqr(f[i]-f[j]-1-L);
while(l < r && slope(q[r],q[r-1]) > slope(i,q[r-1]))r--;//满足队尾斜率单调性
q[++r] = i;//入队
}
printf("%lld\n",(ll)d[n]);
return 0;
}
P2120 [ZJOI2007]仓库建设
题意:$1\sim N$ 号工厂,第$i$ 个工厂有$P_i$个成品,第$i$个工厂建立仓库需要$C_i$的费用,该工厂距离第一个工厂的距离为$X_i$,编号小的工厂只能往编号大的工厂搬用成品,每单位成品搬每单位距离需要花费1,问所有成品搬到工厂里面所需的最少费用是多少
分析 设$f[i]$ 为第 i 个工厂建立仓库,前 i 个工厂的成品都搬到仓库中的最小花费,则容易得到动态转移方程: \(f[i] = min(f[j] + P_{j+1}(X_i-X_{j+1}) + P_{j+2}(X_i-X_{j+2})+\cdots + P_{i-1}(X_i-X_{i-1}))+C_i\)
通式为 \(f[i]=min(f[j]+\sum_{k=j+1}^{i-1}P_k\cdot X_i-\sum_{k=j+1}^{i-1}P_k\cdot X_k)+C_i\)
令 $s[i] = \sum_1^i P[i], ~~g[i] = \sum_1^iP_i\cdot X_i$, 则方程变为 \(f[i] = min(f[j] + X_i\cdot (s[i-1]-s[j])-(g[i-1]-g[j]))+C_i\)
则对于最优决策 $j$ ,有
\[f[j]+g[j]=X_i\cdot s[j]+f[i]-X_i\cdot s[i-1]-C_i\]也就是要找 $y = kx+b$,$k$已知,找一对$x,y$使得截距最小 由于$X[i]$是随$i$递增的,所以要维护的决策集的斜率也是递增的
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
typedef long long ll;
ll C[N],P[N],X[N],f[N],s[N],g[N];
int n;
int q[N],l,r;
long double slope(int i,int j){
return (long double)((f[i]+g[i]) - (f[j]+g[j]))/(s[i]-s[j]);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld",&X[i],&P[i],&C[i]);
s[i] = s[i-1] + P[i];
g[i] = g[i-1] + P[i] * X[i];
}
l = r = 0;
for(int i=1;i<=n;i++){
while(l < r && slope(q[l],q[l+1]) <= X[i])l++;
int j = q[l];
f[i] = f[j] + (s[i-1] - s[j]) * X[i] - g[i-1] + g[j] + C[i];
while(l < r && slope(q[r-1],q[r]) > slope(q[r-1],i))r--;
q[++r] = i;
}
printf("%lld\n",f[n]);
return 0;
}