数据结构进阶(一)
主讲人:孙翔
线段树
一:为什么要线段树?
题目一: 10000个正整数,编号1到10000,用A[1],A[2],A[10000]表示。 修改:无 统计:1.编号从L到R的所有数之和为多少? 其中1<= L <= R <= 10000.
方法一:对于统计L,R ,需要求下标从L到R的所有数的和,从L到R的所有下标记做[L..R],问题就是对A[L..R]进行求和。这样求和,对于每个询问,需要将(R-L+1)个数相加。
方法二:更快的方法是求前缀和,令 S[0]=0, S[k]=A[1..k] ,那么,A[L..R]的和就等于S[R]-S[L-1],这样,对于每个询问,就只需要做一次减法,大大提高效率。
题目二: 10000个正整数,编号从1到10000,用A[1],A[2],A[10000]表示。 修改:1.将第L个数增加C (1 <= L <= 10000) 统计:1.编号从L到R的所有数之和为多少? 其中1<= L <= R <= 10000.
再使用方法二的话,假如A[L]+=C之后,S[L],S[L+1],,S[R]都需要增加C,全部都要修改,见下表。

从上表可以看出,方法一修改快,求和慢。 方法二求和快,修改慢。那有没有一种结构,修改和求和都比较快呢?答案当然是线段树。
二:定义
线段树是一种基于分治思想的二叉树结构,用于在区间上进行信息统计。与按照二进制位(2的次幂)进行区间划分的树状数组相比,线段树是一种更加通用的结构。
1.线段树的每个节点都代表一个区间。
2.线段树具有唯一的根节点,代表的区间是整个统计范围。
3.线段树的每个叶节点都代表一个长度为1的元区间[x,x]。
4.对于每个内部节点[l,r],它的左子节点是[l,mid],右子节点是[mid+1,r],其中mid=(l+r)/2。
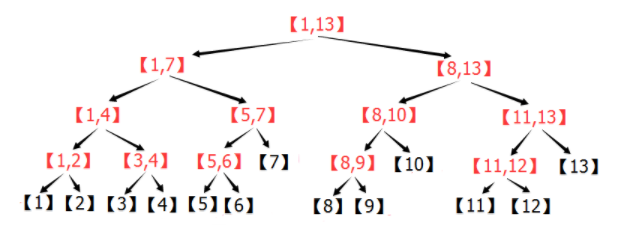
如上图所示为一棵线段树。可以发现,除去树的最后一层,整棵线段树一定是一棵完全二叉树,数的深度是O(logN)。因此,我们可以按照与二叉堆类似的方法建树:
1.根节点的编号为1。
2.编号为x的节点的左子节点编号为x * 2,右子节点编号为x * 2 + 1。
这样我们就能简单地使用一个结构体数组来保存线段树。当然,树的最后一层节点在数组中保存的位置不是连续的,直接空出数组中多余的位置即可。那么,N个叶子节点的满二叉树有N+N/2+N/4…..+2+1=2N-1个节点。由于在最后一层可能还有剩余,因此保存线段树的数组长度不小于4N才能保证不越界。
三:线段树建树
线段树的基本用途是对序列进行维护,支持查询与修改指令。给定一个长度为N的序列A,我们可以在区间[1,N]上建立一棵线段树,每个叶子结点[i,i]保存A[i]的值。线段树的二叉树结构可以很方便地从下往上传递信息。以区间最大值问题为例,记dat(l,r)等于max{A[i]},l<=i<=r。显然dat(l,r)=max(dat(l,mid),dat(mid+1,r))。
下面这段代码建立了一棵线段树并在每个节点上保存了对应区间的最大值。
struct SegmentTree
{
int l,r;
int dat;
}t[SIZE*4]; //结构体数组存储线段树
void build(int p,int l,int r)
{
t[p].l=l,t[p].r=r; //节点p代表区间[l,r]
if(l==r) //叶子节点
{
t[p].dat=a[l];
return ;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
t[p].dat=max(t[p*2].dat,t[p*2+1].dat); //从下往上传递信息
}
build(1,1,n); //调用入口
四:线段树的单点修改
单点修改是一条形如”C x y”的指令,表示把A[x]的值修改为v。
在线段树中,根节点(即编号为1的点)是执行各种指令的入口。我们需要从根节点出发,递归找到代表区间[x,x]的叶子节点,然后从下往上更新[x,x]以及它的所有祖先上保存的信息。容易知道,其时间复杂度也是O(logN)。
void change(int p,int x,int v)
{
if(t[p].l==t[p].r)
{
t[p].dat=v;
return ;
}
int mid=(t[p].l+t[p].r)/2;
if(x<=mid)
{
change(p*2,x,v);
}
else
{
change(p*2+1,x,v);
}
t[p].dat=max(t[p*2].dat,t[p*2+1].dat); //从下往上更新信息
}
change(1,x,v);
五:线段树的区间查询
区间查询是一条形如”Q l r”的指令,例如查询序列A在区间[l,r]上的最大值,即max{A[i]},l<=i<=r。我们只需要从根节点开始,递归执行如下过程。
1.若[l,r]完全覆盖了当前节点代表的区间,则立即回溯,并且该节点的dat值为候选答案。
2.若左子节点与[l,r]有重叠部分,则递归访问左子节点。
3.若右子节点与[l,r]有重叠部分,则递归访问右子节点。
int ask(int p,int l,int r)
{
if(l<=t[p].l&&r>=t[p].r) //完全包含
return t[p].dat;
int mid=(l+r)/2;
int val=-(1<<30); //负无穷
if(l<=mid)
{
val=max(val,ask(p*2,l,r));
}
if(r>mid)
{
val=max(val,ask(p*2+1,l,r));
}
return val;
}
cout<<ask(1,1,r)<<endl;
例题
给定长度为N的数列A,以及M条指令 (N≤500000, M≤100000),每条指令可能是以下两种之一:
“1 x y”,查询区间 [x,y] 中的最大连续子段和,即 max(x≤l≤r≤y) { ∑(i=l~r) A[i] }。
“2 x y”,把 A[x] 改成 y。
分析
针对操作1,在线段树上的每个节点上,除了区间端点外,再维护4个信息:区间和sum,区间最大连续字段和dat,紧靠左端的最大连续字段和lmax,紧靠右端的最大连续子弹和rmax。则得到如下式子:
t[p].sum=t[p*2].sum+t[p*2+1].sum;
t[p].lmax=max(t[p*2].lmax,t[p*2].sum+t[p*2+1].lmax);
t[p].rmax=max(t[p*2].rmax,t[p*2+1].sum+t[p*2].rmax);
t[p].dat=max(t[p*2].dat,t[p*2+1].dat,t[p*2].rmax+t[p*2+1].lmax);
针对操作2,单点修改即可。
六:区间修改
在线段树的“区间修改”指令中,如果某个节点被修改区间[l,r]完全覆盖,那么以该节点为根的整棵子树中的所有节点存储的信息都要修改,若一个一个更新(单点修改),时间复杂度是O(N)的,我们难以接受。
试想一下如果在一次修改指令中发现节点p代表的区间[pl,pr]被修改区间[l,r]完全覆盖,并且一个一个更新了子树p的所有节点,但是在之后的查询指令中却没有用到[l,r]的子区间作为候选答案,那么更新p的整棵子树就是徒劳的。
那么我们考虑在执行修改指令的时候,可以在l<=pl<=pr<=r的情况下立即返回,但是在回溯之前给p节点加一个标记,表示该节点曾经被修改,但是其子节点还没有被修改。
如果在后续的指令中,需要从节点p向下递归,我们再检查p是否有标记。如果有标记,就根据标记信息更新p的两个子节点,同时为p的两个子节点增加标记,然后清除p的标记。
也就是说,除了在修改指令中直接划分的O(logN)个节点外,对任意节点的修改都延迟到在后续操作中递归进入它的父亲节点时再执行。这样,查询和修改指令的时间复杂度都降到了O(logN)。延迟标记提供了线段树中从上向下传递信息的方式。也是设计算法和解决问题的一个重要思路。
struct SegmentTree
{
int l,r;
long long int sum,add;
#define l(x) tree[x].l;
#define r(x) tree[x].r;
#define sum(x) tree[x].sum
#define add(x) tree[x].add
}tree[100010*4];
int a[100010],n,m;
void build(int p,int l,int r)
{
l(p)=l;
r(p)=r;
if(l==r)
{
sum(p)=a[l];
return ;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
sum(p)=sum(p*2)+sum(p*2+1);
}
void spread(int p)
{
if(add(p)) //如果p节点有标记
{
sum(p*2)+=add(p)*(r(p*2)-l(p*2)+1); //更新左子节点信息
sum(p*2+1)+=add(p)*(r(p*2+1)-l(p*2+1)+1); //更新右子节点
add(p*2)+=add(p); //给左子节点打延迟标记
add(p*2+1)+=add(p); //给右子节点打延迟标记
add(p)=0; //清除p的标记
}
}
void change(int p,int l,int r,int d)
{
if(l<=l(p)&&r>=r(p))
{
sum(p)+=(long long int)d*(r(p)-l(p)+1);
add(p)+=d;
return ;
}
spread(p);
int mid(l(p)+r(p))/2;
if(l<=mid)
change(p*2,l,r,d);
if(r>mid)
change(p*2+1,l,r,d);
sum(p)=sum(p*2)+sum(p*2+1);
}
long long int ask(int p,int l,int r)
{
if(l<=l(p)&&r>=r(p))
return sum(p);
spread(p);
int mid=(l+r)/2;
long long int val=0;
if(l<=mid)
val+=ask(p*2,l,r);
if(r>mid)
val+=ask(p*2+1,l,r);
return val;
}
例题:POJ3468
题意:给定长度为N(N<=1e5)的数列A,然后输入Q(Q<=1e5)行操作指令。
第一类指令形如”C l r d”,表示把数列中的第l~r个数都加d。
第二类指令形如”Q l r”,表示询问数列中第l~r个数的和。
分析:区间修改裸题,区间修改时加一个lazy下标即可。
Billboard
题意:有一块h * w的矩形广告板,要往上面贴广告;然后给n个1 * wi的广告,要求把广告贴上去;而且要求广告要尽量往上贴并且尽量靠左;求第n个广告的所在的位置,不能贴则为-1;
分析:利用线段树可以求区间的最大值;将位置即h用来建树(h<=n,大了没有意义);树中存储的为该位置还拥有的空间;若左子树的最大值大于他,就查询左子树,否则查询右子树
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
#define maxn 200010 //元素总个数
int A[maxn<<2];//存原数组数据下标[1,n]
int h,w,n;
//Build函数建树
void Build(int l,int r,int rt)//l,r表示当前节点区间,rt表示当前节点编号
{
A[rt]=w;
if(l==r) //若到达叶节点
{
return;
}
int m=(l+r)>>1;
//左右递归建树
Build(l,m,rt<<1);
Build(m+1,r,rt<<1|1);
}
int Query(int x,int l,int r,int rt)//x表示要查询的值,l,r表示当前节点区间,rt表示当前节点编号
{
if(l==r)
{
A[rt]-=x;
return l;
}
int m=(l+r)>>1;
int res;
if(A[rt<<1]>=x)
{
res=Query(x,l,m,rt<<1);
}
else
{
res=Query(x,m+1,r,rt<<1|1);
}
A[rt]=max(A[rt<<1],A[rt<<1|1]);
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
while(~scanf("%d%d%d",&h,&w,&n))
{
if(h>n)
h=n;
Build(1,h,1);//从1-h建树,根节点是1
while(n--)
{
int x;
scanf("%d",&x);
if(A[1]<x)
{
printf("-1\n");
}
else
{
int ans=Query(x,1,h,1);
printf("%d\n",ans);
}
}
}
return 0;
}
例题
题意:给定一个字符串(长度<=100000),有两个操作。 1:改变某个字符。 2:判断某个子串是否构成回文串。
分析:直接判断是不是字符串必定超时,所以考虑用线段树维护字符串哈希。对于一个字符串a[0],a[1],…,a[n-1] 它对应的哈希函数为a[0]+a[1]K + a[2]K^2 +…+a[n-1]K^(n-1)。** **再维护一个从右往左的哈希值:a[0]K^(n-1) + a[1]*K^(n-2) +…+a[n-1] 若是回文串,则左右的哈希值会相等。而左右哈希值相等,则很大可能这是回文串。
若出现误判,可以再用一个K2,进行二次哈希判断,可以减小误判概率。
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
#define ull __int64
#include<iostream>
using namespace std ;
const int maxn = 100010;
const int x = 123;
ull sum[2][maxn<<2];
ull h[maxn],p[maxn];
char s[maxn];
void push_up ( int rt , int flag )
{
sum[flag][rt] = sum[flag][rt<<1] + sum[flag][rt<<1|1] ;
}
void build ( int l , int r , int rt , int flag ) //1,n,1,0
{
sum[flag][rt] = 0;
if ( l == r )
{
sum[flag][rt] = h[l] ;
return ;
}
int m = ( l + r ) >> 1 ;
build ( lson , flag ) ;
build ( rson , flag ) ;
push_up ( rt , flag ) ;
}
void update ( int a , ull b , int l , int r , int rt , int flag )
{
if ( l == r )
{
sum[flag][rt] = b ;
return ;
}
int m = ( l + r ) >> 1 ;
if ( a <= m )
update ( a , b , lson , flag ) ;
else
update ( a , b , rson , flag ) ;
push_up ( rt , flag ) ;
}
ull query ( int a , int b , int l , int r , int rt , int flag ) //要查询的范围a,b 从1-n查 根是1 flag判断正反哈希建树
{
if ( a <= l && r <= b )
return sum[flag][rt] ;
int m = ( l + r ) >> 1 ;
ull ret = 0 ;
if ( a <= m )
ret += query ( a , b , lson , flag ) ;
if ( m < b )
ret += query ( a , b , rson , flag ) ;
return ret ;
}
int main ()
{
int i , j , k , m , a , b , c , d ;
char op[111] ;
while ( scanf ( "%s" , s ) != EOF ) //输入原字符串
{
scanf ( "%d" , &m ) ;//m个操作
//哈希
int len = strlen ( s ) ;
p[0] = 1 ;
for ( i = 1 ; i <= len ; i ++ )
p[i] = p[i-1] * x ;
for ( i = 0 ; i < len ; i ++ )
h[i+1] = p[i] * (ull) s[i] ;
int n = len ;
build ( 1 , n , 1 , 0 ) ;//flag用于正反哈希的判别
reverse ( s , s + len ) ;
for ( i = 0 ; i < len ; i ++ )
h[i+1] = p[i] * (ull) s[i] ;
build ( 1 , n , 1 , 1 ) ;//反着再哈希一次建树
while ( m -- )
{
scanf ( "%s" , op ) ;
if ( op[0] == 'p' )
{
scanf ( "%d%d" , &a , &b ) ;
ull k1 = query ( a , b , 1 , n , 1 , 0 ) ;
int l = len - b + 1 , r = len - a + 1 ;//反向哈希之后的a,b
ull k2 = query ( l , r , 1 , n , 1 , 1 ) ;
int t1 = a - 1 , t2 = len - b ;
if ( t2 > t1 )
k1 *= p[t2-t1] ;
else
k2 *= p[t1-t2] ;
if ( k1 == k2 )
puts ( "Yes" ) ;
else
puts ( "No" ) ;
}
else
{
scanf ( "%d%s" , &a , op ) ;
update ( a , (ull) p[a-1] * op[0] , 1 , n , 1 , 0 ) ;
update ( len - a + 1 , (ull) p[len-a] * op[0] , 1 , n , 1 , 1 ) ;
}
}
}
return 0 ;
}
七:总结
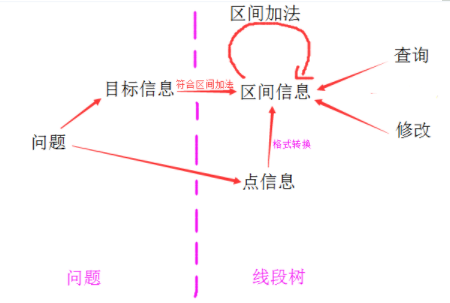
一:将问题转换成点信息和目标信息。即,将问题转换成对一些点的信息的统计问题。
二:将目标信息根据需要扩充成区间信息 1.增加信息符合区间加法。 2.增加标记支持区间操作。
三:代码中的主要模块: 1.区间加法 2.标记下推 3.点信息->区间信息 4.操作(各种操作,包括修改和查询)
完成第一步之后,题目有了可以用线段树解决的可能。 完成第二步之后,题目可以由线段树解决。
第三步就是慢慢写代码了。
解题模型如图所示:
扫描线
线段树的一大应用是扫描线。
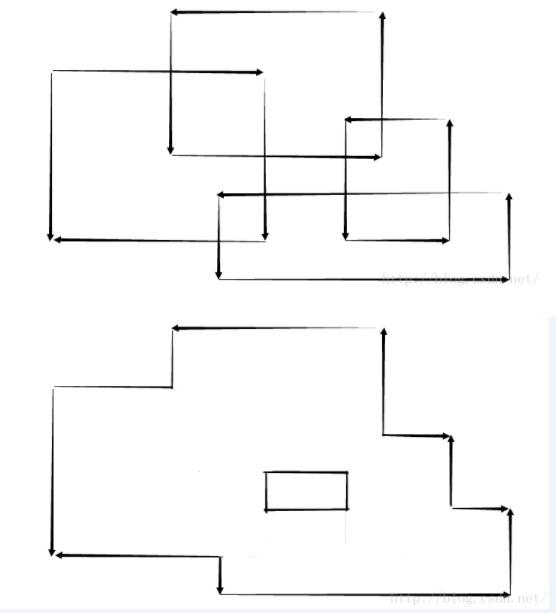
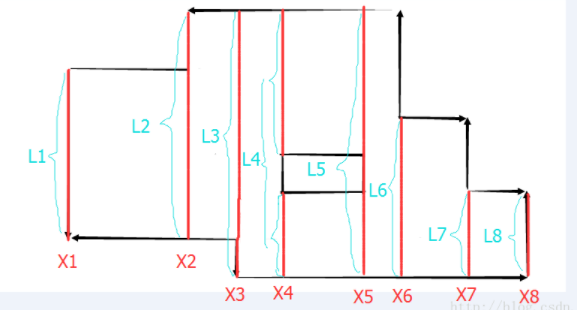
观察第三个图: 扫描线的思路:使用一条垂直于X轴的直线,从左到右来扫描这个图形,明显,只有在碰到矩形的左边界或者右边界的时候,这个线段所扫描到的情况才会改变,所以把所有矩形的入边,出边按X值排序。然后根据X值从小到大去处理,就可以用线段树来维护扫描到的情况。如上图,X1到X8是所有矩形的入边,出边的X坐标。而红色部分的线段,是这样,如果碰到矩形的入边,就把这条边加入,如果碰到出边,就拿走。红色部分就是有线段覆盖的部分。要求面积,只需要知道图中的L1到L8。而线段树就是用来维护这个L1到L8的。
算法流程:
X1:首先遇到X1,将第一条线段加入线段树,由线段树统计得到线段长度为L1.
X2:然后继续扫描到X2,此时要进行两个动作: 1.计算面积,目前扫过的面积=L1*(X2-X1) 2.更新线段。由于X2处仍然是入边,所以往线段树中又加了一条线段,加的这条线段可以参考3幅图中的第一幅。然后线段树自动得出此时覆盖的线段长度为L2 (注意两条线段有重叠部分,重叠部分的长度只能算一次)。
X3:继续扫描到X3,步骤同X2,先计算 扫过的面积+=L2*(X3-X2),再加入线段,得到L3。
X4:扫描到X4有些不一样了。首先还是计算 扫过的面积+=L3*(X4-X3),然后这时遇到了第一个矩形的出边,这时要从线段树中删除一条线段。删除之后的结果是线段树中出现了2条线段,线段树自动维护这两条线段的长度之和L4。
思考:线段树进行线段操作时,每个点的含义应该是什么?
线段树如果没有离散化,那么线段树下标为1,就代表线段[1,2) 线段树下标为K的时候,代表的线段为[K,K+1) (长度为1) 所以,将上面的所有线段都化为[y1,y2)就可以理解了,线段[y1,y2)只包括线段树下标中的y1,y1+1,…,y2-1
当y值的范围是10^9时,就不能再按照上面的办法按值建树了,这时需要离散化。
其实就是把每条边提前找到存到一个数组里面,让叶子节点维护的不是长度1,而是对应的一个高度。
#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 201
struct Node
{
int l,r;//线段树的左右整点
int c;//c用来记录重叠情况
double cnt,lf,rf;
//cnt用来计算实在的长度,rf,lf分别是对应的左右(上下)真实的浮点数端点
}segTree[MAXN*3];
struct Line
{
double x,y1,y2;
int f;//入边还是出边,1入,-1出
}line[MAXN];
//把一段段平行于y轴的线段表示成数组 ,
//x是线段的x坐标,y1,y2线段对应的下端点和上端点的坐标
//一个矩形 ,左边的那条边f为1,右边的为-1,
//用来记录重叠情况,可以根据这个来计算,nod节点中的c
bool cmp(Line a,Line b)//sort排序的函数
{
return a.x < b.x;
}
double y[MAXN];//记录y坐标的数组
void Build(int t,int l,int r)//构造线段树,t是当前节点 1,1,t-1
{
segTree[t].l=l;segTree[t].r=r;
segTree[t].cnt=segTree[t].c=0;
segTree[t].lf=y[l];
segTree[t].rf=y[r];
if(l+1==r)
return;
int mid=(l+r)>>1;
Build(t<<1,l,mid);
Build(t<<1|1,mid,r);//递归构造
}
void calen(int t)//计算长度
{
if(segTree[t].c>0)
{
//cout<<"123"<<endl;
segTree[t].cnt=segTree[t].rf-segTree[t].lf;
return;
}
if(segTree[t].l+1==segTree[t].r)
{
//cout<<"456"<<endl;
segTree[t].cnt=0;
}
else
{
//cout<<"789"<<endl;
segTree[t].cnt=segTree[t<<1].cnt+segTree[t<<1|1].cnt;
}
}
void update(int t,Line e)//加入线段e,后更新线段树 1,line[1]
{
if(e.y1==segTree[t].lf&&e.y2==segTree[t].rf)//找到对应的边
{
segTree[t].c+=e.f;
//cout<<"segTree[t].c:"<<segTree[t].c<<endl;
calen(t);
return;
}
if(e.y2<=segTree[t<<1].rf) update(t<<1,e);
else if(e.y1>=segTree[t<<1|1].lf) update(t<<1|1,e);
else
{
Line tmp=e;
//cout<<"e.y2:"<<e.y2<<" e.y1:"<<e.y1<<" e.f:"<<e.f<<endl;
//cout<<"tmp.y2:"<<tmp.y2<<" tmp.y1:"<<tmp.y1<<" tmp.f:"<<tmp.f<<endl;
tmp.y2=segTree[t<<1].rf;
update(t<<1,tmp);
tmp=e;
tmp.y1=segTree[t<<1|1].lf;
update(t<<1|1,tmp);
}
//cout<<"999999999segTree[t].c:"<<segTree[t].c<<endl;
calen(t);
}
int main()
{
int i,n,t,Case=0;
double x1,y1,x2,y2;
while(scanf("%d",&n),n)
{
Case++;
t=1;
for(i=1;i<=n;i++)
{
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
line[t].x=x1;
line[t].y1=y1;
line[t].y2=y2;
line[t].f=1;//一开始入边
y[t]=y1;//y点坐标
t++;
line[t].x=x2;
line[t].y1=y1;
line[t].y2=y2;
line[t].f=-1;//出边
y[t]=y2;
t++;
}
sort(line+1,line+t,cmp);//输入完之后根据x坐标对所有的线段排序
sort(y+1,y+t); //对y点从小到大排序
Build(1,1,t-1);
update(1,line[1]);
double res=0;
for(i=2;i<t;i++)
{
res+=segTree[1].cnt*(line[i].x-line[i-1].x);
update(1,line[i]);
}
printf("Test case #%d\nTotal explored area: %.2f\n\n",Case,res);
}
return 0;
}
那么如果是求所有矩形围成的图形的周长呢?
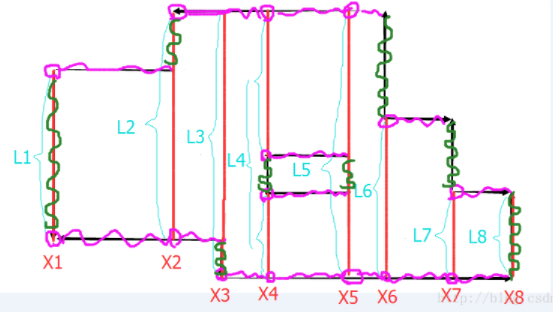
这个图是在原来的基础上多画了一些东西,这次是要求周长。 所有的横向边都画了紫色,所有的纵向边画了绿色。
先考虑绿色的边,由图可以观察到,绿色边的长度其实就是L的变化值。 比如考虑X1,本来L是0,从0变到L1,所以绿色边长为L1. 再考虑X2,由L1变成了L2,所以绿色边长度为L2-L1, 于是,绿色边的长度就是L的变化值(注意上图中令L0=0,L9=0)。 因为长度是从0开始变化,最终归0.
再考虑紫色的边,要计算紫色边,其实就是计算L的线段是有几个线段组成的,每个线段会贡献两个端点(紫色圆圈) 而每个端点都会向右延伸出一条紫色边一直到下一个X值。
所以周长就是以上两部分的和。
#include<stdio.h>
#include<iostream>
#include<algorithm>
#define LEN 10010
using namespace std;
struct Node
{
int left;
int right;
int count;//被覆盖次数
int line;//所包含的区间数量
int lbd;//左端点是否被覆盖
int rbd;//右端点是否被覆盖
int len;//长度
};
struct ScanLine
{
int x;
int y1;
int y2;
int flag;
};
struct Node node[LEN*4];
struct ScanLine scan[LEN];
int y[LEN];
void build(int l, int r, int i)//0 n-1 1
{
node[i].left = l;
node[i].right = r;
node[i].count = 0;
node[i].len = 0;
node[i].line = 0;
if (r - l > 1)
{
int mid = (l + r)/2;
build(l, mid, 2*i);
build(mid, r, 2*i + 1);
}
}
//更新测度m
void update_len(int i)
{
if (node[i].count > 0)
node[i].len = y[node[i].right] - y[node[i].left];
else if (node[i].right - node[i].left == 1)
node[i].len = 0;
else
{
node[i].len = node[2*i].len + node[2*i + 1].len;
}
}
//更新line
void update_line(int i)
{
if (node[i].count > 0)
{
node[i].lbd = 1;
node[i].rbd = 1;
node[i].line = 1;
}
else if (node[i].right - node[i].left == 1)
{
node[i].lbd = 0;
node[i].rbd = 0;
node[i].line = 0;
}
else
{
node[i].lbd = node[2*i].lbd;
node[i].rbd = node[2*i + 1].rbd;
node[i].line = node[2*i].line + node[2*i + 1].line - node[2*i].rbd*node[2*i + 1].lbd;
//cout<<"node[i].lbd:"<<node[i].lbd<<" node[i].rbd:"<<node[i].rbd<<endl;
}
}
void insert(int l, int r, int i) //y1,y2,1
{
//在这里要取离散化之前的原值进行比较
if (y[node[i].left] >= l && y[node[i].right] <= r)
(node[i].count)++;
else if (node[i].right - node[i].left == 1)
return;
else
{
int mid = (node[i].left + node[i].right)/2;
if (r <= y[mid])
insert(l, r, 2*i);
else if (l >= y[mid])
insert(l, r, 2*i + 1);
else
{
insert(l, y[mid], 2*i );
insert(y[mid], r, 2*i + 1);
}
}
update_len(i);
update_line(i);
}
void remove(int l, int r, int i)
{
//在这里要取离散化之前的原值进行比较
if (y[node[i].left] >= l && y[node[i].right] <= r)
(node[i].count)--;
else if (node[i].right - node[i].left == 1)
return;
else
{
int mid = (node[i].left + node[i].right)/2;
if (r <= y[mid])
remove(l, r, 2*i );
else if (l >= y[mid])
remove(l, r, 2*i + 1);
else
{
remove(l, y[mid], 2*i );
remove(y[mid], r, 2*i + 1);
}
}
update_len(i);
update_line(i);
}
bool cmp(struct ScanLine line1, struct ScanLine line2)
{
if (line1.x == line2.x)
return line1.flag > line2.flag;
return (line1.x < line2.x);
}
int main()
{
int n;
scanf("%d", &n);
int x1, y1, x2, y2;
int i = 0;
while (n--)
{
scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
scan[i].x = x1;
scan[i].y1 = y1;
scan[i].y2 = y2;
scan[i].flag = 1;
y[i++] = y1;
scan[i].x = x2;
scan[i].y1 = y1;
scan[i].y2 = y2;
scan[i].flag = 0;
y[i++] = y2;
}
sort(y, y + i);
sort(scan, scan + i, cmp);
//y数组中不重复的个数
int unique_count = unique(y, y + i) - y;
/*
for(int i=1;i<n*2;i++)//Y数组去重
{
if(Index[i]!=Index[i-1])
Index[cnt++]=Index[i-1];
}
Index[cnt++]=Index[2*n-1];//这里很容易错!
*/
//离散化,建立线段树
build(0, unique_count - 1, 1);
int perimeter = 0;
int now_len = 0;
int now_line = 0;
for (int j = 0; j < i; j++)
{
if (scan[j].flag)
insert(scan[j].y1, scan[j].y2, 1);
else
remove(scan[j].y1, scan[j].y2, 1);
if (j >= 1)
perimeter += 2*now_line*(scan[j].x - scan[j-1].x);
perimeter += abs(node[1].len - now_len);
now_len = node[1].len;
now_line = node[1].line;
}
printf("%d\n", perimeter);
return 0;
}
笛卡尔树
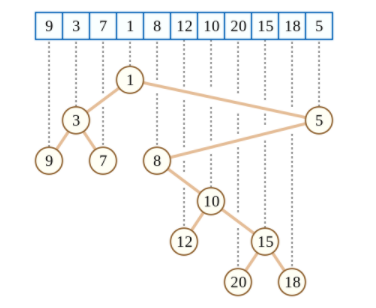
笛卡尔树是形如上图的一棵树,满足 ①堆的性质,如本图,小根堆,两子的值大于等于父亲的值 ②二叉搜索树性质,即左子树的点key(默认为下标)比根小,右子树的点key(默认为下标)比根大 显然,按中序遍历这棵树,可得原序列 ③询问下标i到下标j之间(i<j)的最小值,只需寻找[i,j]的lca
可由数列构造,在范围最值查询、范围top k查询(range top k queries)等问题上有广泛应用。它具有堆的有序性,中序遍历可以输出原数列
笛卡尔树比较难的地方在于构造,这里给出大概的思路。
笛卡尔树模板: 从前往后遍历A[i], 1.对于每一个A[i],从栈中找出(从栈顶往栈底遍历,或者从数组后往前遍历)第一个小于等于A[i]的元素 2.如果找到,i.parent为sta[k],同时sta[k].r=i,即i为sta[k]的右子树, 3.如果栈中存在比A[i]大的元素 这些元素肯定是出栈了,这个问题最后的代码统一表示。 同时,sta[k+1].parent=i; i.l=sta[k+1] 即sta[K+1]为i的左子树 4.最后i入栈,比i大的A[i]都自动出栈了
#include <iostream>
#include <queue>
using namespace std;
const int maxnum=11;
int a[maxnum];
struct node
{
int key;
int parent;
int l;
int r;
}tree[maxnum];
void Init()
{
int i;
for(i=0;i<maxnum;i++)
tree[i].parent=tree[i].l=tree[i].r=-1; //初始化
}
int Build_Tree()
{
int i,top,k;
int stack[maxnum];
top=-1;
for(i=0;i<maxnum;i++)
{
k=top;
while(k>=0 && a[stack[k]]>a[i]) //栈中比当前元素大的都出栈
k--;
if(k!=-1) //find it,栈中元素没有完全出栈,当前元素为栈顶元素的右孩子
{
tree[i].parent=stack[k];
tree[stack[k]].r=i;
}
if(k<top) //出栈的元素为当前元素的左孩子
{
tree[stack[k+1]].parent=i;
tree[i].l=stack[k+1];
}
stack[++k]=i;//当前元素入栈
top=k;//top指向栈顶元素
}
tree[stack[0]].parent=-1;//遍历完成后的栈顶元素就是根
return stack[0];
}
void inorder(int node)
{
if(node!=-1)
{
inorder(tree[node].l);
cout<<tree[node].key<<" ";
inorder(tree[node].r);
}
}
void levelorder(int node)
{
queue<int> q;
q.push(node);
while(!q.empty())
{
int k=q.front();
q.pop();
cout<<tree[k].key<<" ";
if(tree[k].l!=-1)
q.push(tree[k].l);
if(tree[k].r!=-1)
q.push(tree[k].r);
}
}
int main()
{
int i;
Init();
for(i=0;i<maxnum;i++)
{
cin>>a[i];
tree[i].key=a[i];
}
int root=Build_Tree();
cout<<root<<endl;
inorder(root); //中序遍历
cout<<endl;
levelorder(root); //层序遍历
cout<<endl;
return 0;
}
/*
3 2 4 5 6 8 1 9 1 0 7
*/
例题:牛客多校第一场
题意:给两个数组a和b,让你找最大的p坐标使得1到p这个范围中,a和b数组里面的最小值的下标一样。
分析:根据笛卡尔树的性质,那不就是求一个最大的下标p,使得两个序列构建的笛卡尔树同构。问题变得简单清晰,直接二分p坐标即可
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+10;
stack<int> s;
int a[maxn],b[maxn],l[2][maxn],r[2][maxn],rt[2];
//找最大的p,使得a,b两数组中1-p范围内,最小元素的下标相同
int di(int n)
{
for(int i=1;i<=n;i++)
{
l[0][i]=r[0][i]=0;
while((!s.empty())&&(a[i]<a[s.top()]))//i对应的元素值最大,a[i]为父节点,小根堆
l[0][i]=s.top(), s.pop();//如果a[i]小于根节点,则将a[i]作为根节点的父节点
if(!s.empty())//如果a[i]大于根节点,则从根节点的右节点去找位置
r[0][s.top()]=i;
s.push(i);
}
while(!s.empty())
rt[0]=s.top(), s.pop();
for(int i=1;i<=n;i++)
{
l[1][i]=r[1][i]=0;
while((!s.empty())&&(b[i]<b[s.top()]))
l[1][i]=s.top(), s.pop();
if(!s.empty())
r[1][s.top()]=i;
s.push(i);
}
while(!s.empty())
rt[1]=s.top(), s.pop();
for(int i=1;i<=n;i++)//ab两个数组构成的笛卡尔树一样则可以
if(l[0][i]!=l[1][i]||r[0][i]!=r[1][i])
return 0;
return 1;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
while(cin>>n)
{
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<=n;i++)
cin>>b[i];
int L=1,R=n;
while(L<R)//二分找最大的符合条件的下标
{
int mid=(L+R)/2;
if(di(mid))
L=mid+1;
else
R=mid;
}
if(!di(L))
L--;
cout<<L<<endl;
}
return 0;
}
2018年杭电多校
题意:定义RMQ(A,l,r)为:序列A中,满足A[i] = max(A[l],A[l+1],…,A[r])的最小的i。如果对于任意(l,r)都满足RMQ(A,l,r)=RMQ(B,l,r)则为A和B是RMQ Similar。现在出A序列,B序列的每个数都是0~1之间的实数,问满足与A是RMQ Similar的所有B序列中所有数之和的期望。
分析:不难发现,如果A和B是RMQ相似,那么A和B就是笛卡尔树同构。因为B中的每一个数都是 0~1之间的实数,因此出现相同数字的概率可以认为是0,可以假设B是每个数都不相同的排列。设A的笛卡尔树每个子树大小为sz[i],那么任一B排列和A同构的概率就是sz[i],i从1到n的累乘。又根据题意,B满足均匀分布,因此B的和的期望值是n/2。因此总期望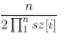
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<stack>
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
stack<int>st;
ll inv[maxn];
int n;
struct node
{
int val,sz;//sz表示size,子树大小
int l,r,par;
}t[maxn];
void init()
{
for(int i=0;i<=n;i++)
t[i].l=0,t[i].r=0,t[i].par=0,t[i].sz=0;//初始化
t[0].val=inf;
while(!st.empty())
st.pop();
st.push(0);
}
void build()
{
for(int i=1;i<=n;i++)
{
while(!st.empty()&&t[st.top()].val<t[i].val)//从栈顶往栈底遍历,
st.pop();
int par=st.top();
t[i].par=par;//i.par为st.pop()
t[i].l=t[par].r;//i的左子树是原来父节点的右节点,因为此点比i先到,且>=i。
t[t[par].r].par=i;
t[par].r=i;//i作为右子树
st.push(i);
}
}
void dfs(int u)//求子树大小
{
if(u==0)
return ;
t[u].sz=1;
dfs(t[u].l);
dfs(t[u].r);
t[u].sz+=t[t[u].l].sz+t[t[u].r].sz;
}
void Inv()//扩展gcd求逆元
{
inv[1]=1;
for(int i=2;i<maxn;i++)
inv[i]=inv[mod%i]*(mod-mod/i)%mod;
}
int main()
{
Inv();
int T;
cin>>T;
while(T--)
{
cin>>n;
init();
for(int i=1;i<=n;i++)
cin>>t[i].val;
build();//建树
dfs(t[0].r);//从0节点的右子树开始,计算每个节点的大小
ll ans=n*inv[2]%mod;//以下就是公式的代码表达。
for(int i=1;i<=n;i++)
ans=ans*inv[t[i].sz]%mod;
cout<<ans<<endl;
}
return 0;
}
二叉搜索树(BST)
1:定义
给定一棵二叉树,树上的每个节点带有一个数值,称为节点的关键码。所谓“BST性质”是指,对于树中的任意一个节点:
1.该节点的关键码不小于它的左子树中任意节点的关键码。
2.该节点的关键码不大于它的右子树中任意节点的关键码。
满足上述性质的二叉树就是一棵“二叉搜索树”。显然,二叉搜索树的中序遍历是一个关键码单调递增的节点序列。
2:BST的建立
为了避免越界,减少边界情况的特殊判断,我们一般在BST中额外插入一个关键码为正无穷和一个关键码为负无穷的节点。仅由这两个节点构成的BST就是一棵初始的空的BST。
struct BST
{
int l, r; //左右孩子节点在数组中的下标
int val; //节点关键码
} a[SIZE];
int tot, root, INF = 1<<30;
int New(int val)
{
a[++tot].val = val;
return tot;
}
void Build()
{
New(-INF), New(INF);
root = 1, a[1].r = 2;
}
3:BST的检索
在BST中检索是否存在关键码为val的节点。设变量p等于根节点root,则执行如下过程:
1.若p的关键码等于val,则已经找到。
2.若p的关键码大于val
(1)若p的左子节点为空,则说明不存在val。
(2)若p的左子节点不为空,则p的左子树中递归进行检索。
3.若p的关键码小于val
(1)若p的右子节点为空,则说明不存在val。
(2)若p的右子节点不为空,在p的右子树中递归检索。
int Get(int p, int val) {
if (p == 0) //检索失败
return 0;
if (val == a[p].val) // 检索成功
return p;
return val < a[p].val ? Get(a[p].l, val) : Get(a[p].r, val);
}
4:BST的插入
在BST中插入一个新的值val(假设目前BST中不存在关键码为val的节点)。那么与BST检索过程类似。
在发现要走向的p的子节点为空,说明val不存在,直接建立关键码为val的新节点作为p的子节点。
void Insert(int &p, int val)
{
if (p == 0)
{
p = New(val); // 注意p是引用,其父亲节点的l和r值会被同时更新
return;
}
if (val == a[p].val)
return;
if (val < a[p].val)
Insert(a[p].l, val);
else
Insert(a[p].r, val);
}
5:BST求前驱和后继
以后继为例。val的后继指的是在BST中关键码大于val的前提下,关键码最小的节点。
初始化ans为具有正无穷关键码的那个节点的编号。然后,在BST中检索val。在检索过程中,没经过一个节点,都检查该节点的关键码,判断能否更新所求的后继ans。
检索完成后,有三种可能的结果:
1.没有找到val。此时val的后继就在已经经过的节点中,ans即为所求。
2.找到了关键码为val的节点p,但是p没有右子树。与上种情况相同,ans即为所求。
3.找到了关键码为val的节点p,且p有右子树。那就从p的右子树出发,一直向左走就找到了。
int GetNext(int val)
{
int ans = 2; // a[2].val==INF
int p = root;
while (p)
{
if (val == a[p].val) // 检索成功
{
if (a[p].r > 0) // 有右子树
{
p = a[p].r;
while (a[p].l > 0) // 右子树一直向左走
p = a[p].l;
ans = p;
}
break;
}
// 每经过一个节点,都尝试更新后继
if (a[p].val > val && a[p].val < a[ans].val)
ans = p;
p = val < a[p].val ? a[p].l : a[p].r;
}
return ans;
}
6:BST的节点删除
从BST中删除关键码为val的节点。
首先,在BST中检索val,得到节点p。
若p的子节点个数小于2,则直接删除p,并令p的子节点 代替p的位置,与p的父节点相连即可。
若p既有左子树又有右子树,则在BST中求出val的后继节点next。因为next没有左子树,所以可以直接删除next,令next的右子树代替next即可。最后让next代替p节点。
void Remove(int &p, int val) //从子树p中删除值为val的节点
{
if (p == 0)
return;
if (val == a[p].val) // 检索到值为val的节点
{
if (a[p].l == 0) // 没有左子树
{
p = a[p].r; // 右子树代替p的位置
}
else if (a[p].r == 0) //没有右子树
{
p = a[p].l; // 左子树代替p的位置
}
else // 既有左子树又有右子树
{
// 求后继节点
int next = a[p].r;
while (a[next].l > 0)
next = a[next].l;
// next一定没有左子树,直接删除
Remove(a[p].r, a[next].val);
// 令next节点代替p节点
a[next].l = a[p].l, a[next].r = a[p].r;
p = next;
}
return;
}
if (val < a[p].val)
{
Remove(a[p].l, val);
}
else
{
Remove(a[p].r, val);
}
}
在随机数据情况下,BST一次操作的期望复杂度是O(logN)。但是,BST很容易退化,试想如果插入一个有序序列,就会得到一条链,那么平均每次操作的复杂度就是O(N)的,这是我们无法忍受的。这种左右子树大小相差很大的BST是不平衡的。有很多方法可以维持BST的平衡,从而产生了各种平衡树。
那么欲知后事如何,请听下回分解。treap,splay。